![]()
(1)
DIE BEUGERBIBEL
© DP Dirk Hauschild
2003-2004 Assistenzbeuger *
2004 - 2008 Chefbeuger *
ab 2008 Privatbeuger #
* TU Chemnitz Professur „Physik dünner Schichten“ (PHDS)
E-Mail: * dirk.hauschild@physik.tu-chemnitz.de
letzte Änderung: Montag, 22. März 2010
1. Physikalische Grundlagen 3
1.1. Kinematische Streutheorie 3
Einschub 1: relativistische Elektronen: 4
Einschub 2: der vernachlässigte letzte Summand 8
Abbruchoszillationen im Ortsraum 10
Abbruchoszillationen im Impulsraum 14
1.2. Übersicht der Formeln 17
Die gestreute Amplitude einer aus N Atomen bestehenden Substanz ergibt sich aus:
|
|
(1) |
Mit den Atompositionen rn und dem Atomformfaktor
![]()
Dieser ist komplex:
|
|
(2) |
![]() ist
die Magnitude und η
die Phase.
ist
die Magnitude und η
die Phase.
Der Formfaktor hängt von der verwendeten Strahlung ab. Für Röntgenstrahlung lautet dieser [1]:
|
|
(3) |
mit![]() der
totalen Ladungsdichte und
der
totalen Ladungsdichte und![]() .
.
Die
Umrechnung von s in Impulsüberträge K
lautet![]() .
Damit ist für die Berechnung des Formfaktors aus Tabellenwerten
die Kenntnis über die Wellenlänge der verwendeten Strahlung
unwichtig. Das einzig wichtige ist die Art der verwendeten Strahlung.
.
Damit ist für die Berechnung des Formfaktors aus Tabellenwerten
die Kenntnis über die Wellenlänge der verwendeten Strahlung
unwichtig. Das einzig wichtige ist die Art der verwendeten Strahlung.
Für Elektronen gilt:
|
|
(4) |
Wenn
die Elektronen eine sehr hohe kinetische Energie haben oder wenn das
Potential![]() klein genug ist kann man die Wellenfunktion
klein genug ist kann man die Wellenfunktion![]() ersetzen durch die ungestörte
Wellenfunktion
ersetzen durch die ungestörte
Wellenfunktion![]() (erste Born-Näherung). Nimmt man zusätzlich an das Atom ist
sphärisch symmetrisch ergibt sich:
(erste Born-Näherung). Nimmt man zusätzlich an das Atom ist
sphärisch symmetrisch ergibt sich:
|
|
(5) |
mit![]() dem
Atompotential, der Differenz zwischen dem Potential erzeugt durch die
Nukleonen und dem durch die Elektronen. Man beachte, dass
dem
Atompotential, der Differenz zwischen dem Potential erzeugt durch die
Nukleonen und dem durch die Elektronen. Man beachte, dass![]() nicht
komplex ist!
nicht
komplex ist!
Gl. 5 gilt nur für neutrale Atome. Für Ionen ändert sich das Atompotential zu:
|
|
(6) |
Damit wird Gl. 5 zu:
|
|
(7) |
Über die Poisson Gleichung kann man beide Formfaktoren ineinander umrechnen:
|
|
(8) |
Bei
einem Streuwinkel von![]() wird
wird
![]() und
Gl. 8 ist nicht lösbar. Werte für diesen Streuwinkel erhält
man durch Extrapolation zu:
und
Gl. 8 ist nicht lösbar. Werte für diesen Streuwinkel erhält
man durch Extrapolation zu:
|
|
(9) |
Mit r, dem Atomradius.
Die Werte für Formfaktoren sind in zahlreichen Werken tabelliert, z.B. [1][2].
Einschub 1: relativistische Elektronen:
Bei den Formfaktoren für Elektronen muss der tabellarisierte Wert noch mit einem Wert multipliziert werden, welcher die relativistische Massenzunahme des Elektrons berücksichtigt. Dieser Faktor ist:
|
|
(10) |
Für Elektronen mit einer Beschleunigungsspannung von UH=-68keV ist dieser Faktor 1,133 (v/c=0,47). Für UH=-200keV (Schultze) ist der Faktor 1,391 (v/c=0,69).
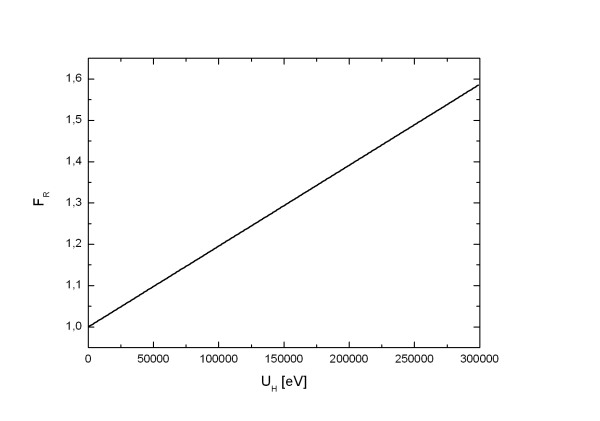
Abbildung
1:
relativistischer Faktor der
Elektronen
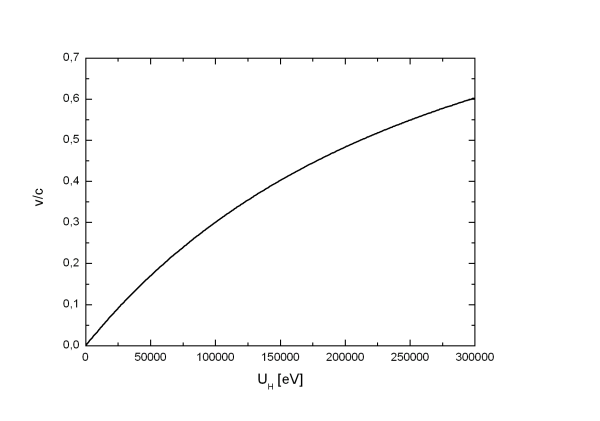
Abbildung
2:
relative Geschwindigkeit der
Elektronen
Auswirkungen:
Eine testweise Auswertung mit den verschiedenen Beschleunigungsspannungen (UH = 0 eV, UH = -68 keV, UH = -200 keV) ergab bei der Dichte eine maximale Abweichung von 0,1%. Die Unterschiede in den Intensitäten sind sogar noch geringer (s. Abb. 4 und 3).
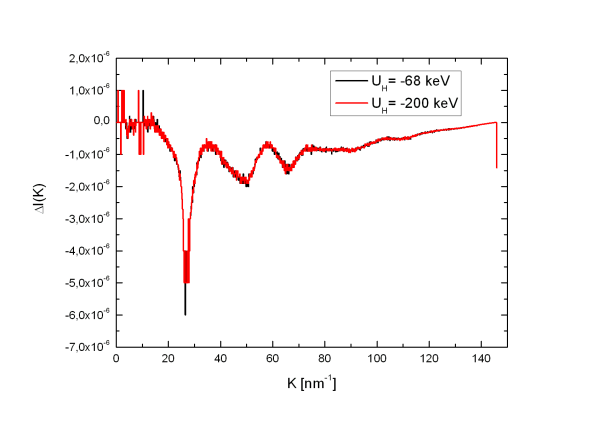
Abbildung
4:
Änderung im I(K)
durch FR
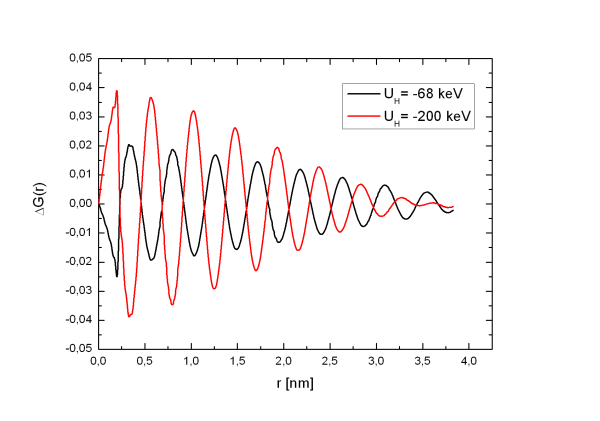
Abbildung
3:
Änderung im G(r)
durch FR
Ende Einschub
Messbar ist jedoch nicht die Amplitude, sondern nur die Streuintensität:
|
|
(11) |
Separiert man den Anteil, der vom gleichen Atom stammt erhält man:
|
|
(12) |
Für Legierungen definiert man gewichtete Atomformfaktoren, in welche die Konzentrationen und die Atomformfaktoren der beteiligten Komponenten eingehen:
|
|
(13) |
mit ci und fi(K) den Konzentrationen bzw. Atomformfaktoren der Komponenten.
Nun
führt man ein
![]() ein,
sodass
ein,
sodass
![]() die
Anzahl der Atomzentren im Volumenelement
die
Anzahl der Atomzentren im Volumenelement
![]() im
Abstand
im
Abstand
![]() vom
Atom m ist. Damit ergibt sich
durch Ersetzung der Summe in Gl. (12)
durch ein Integral über das Probenvolumen Vp
(
vom
Atom m ist. Damit ergibt sich
durch Ersetzung der Summe in Gl. (12)
durch ein Integral über das Probenvolumen Vp
(![]() ):
):
|
|
(14) |
Im
nächsten Schritt wird ein Faktor mit der mittleren Dichte![]() der
Legierung addiert und subtrahiert, so dass Gl. (14) wird zu:
der
Legierung addiert und subtrahiert, so dass Gl. (14) wird zu:
|
|
(15) |
Der letzte Summand kann in den meisten Fällen vernachlässigt werden (siehe S. 8).
Für
einen amorphen Körper, in dem Kugelsymmetrie vorliegt,
vereinfacht sich das erste Integral in Gl. (15) folgendermaßen
(Kugelkoordinaten,![]() „ausgeklammert“):
„ausgeklammert“):
|
|
(16) |
Substitution
von
![]() ergibt
ergibt
|
|
(17) |
Integriert
über
![]() ergibt
sich:
ergibt
sich:
|
|
(18) |
die
Klammer ergibt![]() und
damit:
und
damit:
|
|
(19) |
damit
und mit![]() ,
der reduzierten Dichteverteilung, sowie mit
,
der reduzierten Dichteverteilung, sowie mit
![]() ,
der Atomzahl wird Gl. (15) zu:
,
der Atomzahl wird Gl. (15) zu:
|
|
(20) |
Bzw. zur Debye-Streugleichung [3] (vgl . Gl. (11))
|
|
(21) |
folgende Abkürzung wird verwendet:
|
|
(22) |
I(K) nennt man Interferenzfunktion.
Wenn
die Differenz zwischen den Mittelungen der Formfaktoren
![]() groß,
dann äußert sich dies in der diffusen Lauestreuung [4],
welche einen strukturlosen Anteil zu I(K) beiträgt
und es gilt außerdem
groß,
dann äußert sich dies in der diffusen Lauestreuung [4],
welche einen strukturlosen Anteil zu I(K) beiträgt
und es gilt außerdem![]() ,
sonst gilt
,
sonst gilt
![]() .
.
Der
Term
![]() in
Gl. (22) gibt die Anzahl der Atome an, die im Mittel einen bestimmten
Abstand zu einander haben. Damit ergibt sich kurz:
in
Gl. (22) gibt die Anzahl der Atome an, die im Mittel einen bestimmten
Abstand zu einander haben. Damit ergibt sich kurz:
|
|
(23) |
Würde zwischen den N Atomen der Streusubstanz keine Korrelation bestehen würde man Nf² messen.
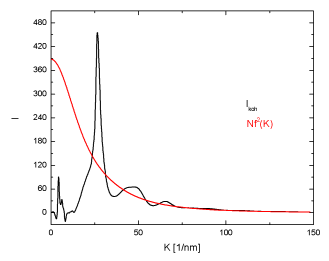
Abbildung
5:
Die entsprechende gesamte gestreute Intensität
wäre
|
|
(24) |
Die amorphe Schicht, bestehend aus N Atomen streut
|
|
(25) |
Daraus folgt
|
|
(26) |
Es
wird zusätzlich noch ein Korrekturterm![]() eingeführt,
der die in
eingeführt,
der die in
![]() bei
der Elektronenbeugung in Transmission nicht beobachtete
Kleinwinkelstreuung berücksichtigt [5][4][6][7]. Damit wird Gl.
26 zu
bei
der Elektronenbeugung in Transmission nicht beobachtete
Kleinwinkelstreuung berücksichtigt [5][4][6][7]. Damit wird Gl.
26 zu
|
|
(27) |
Diese Methode kann nur angewendet werden, wenn bei Kmax keine Oszillationen mehr auftreten [7].
Bei
der Aufnahme des Streuspektrums wird neben![]() auch
der Untergrund U(K) gemessen. Die gesamte Streuintensität
wird mit
auch
der Untergrund U(K) gemessen. Die gesamte Streuintensität
wird mit![]() bezeichnet,
so dass gilt:
bezeichnet,
so dass gilt:
|
|
(28) |
Einschub 2: der vernachlässigte letzte Summand
In Gl. (15) wurde der letzte Summand als vernachlässigbar angesehen, dies wird nun weiter untersucht. Nennen wir diesen Summanden S3.
|
|
(29) |
Unter Verwendung der Gleichungen (16) bis (19) ergibt sich analog
|
|
(30) |
Die obere Integrationsgrenze ergibt sich aus der Integration über die gesamte Probe (bzw. das durchstrahlte Volumen) mit dem Radius RP. Die Integration ergibt:
|
|
(31) |
Unter Kenntnis der Probengeometrie kann man den Einfluß von S3 abschätzen. Die Probe besteht aus einer Aufdampfschicht mit einer typischen Dicke d = 30nm auf einer kreisförmigen Lochblende mit dem Durchmesser 2r = 20μm (Beugungskryos PHDS, beim Schulze ist der Durchmesser anders, fragen!) Aus dem Probenvolumen und dem äquivalenten Kugelradius
|
|
(32) |
folgt RP = 1300nm (Schulze: ...). Aus Gl. (22) und einer Integration analog zu S3 folgt (Integration für große r, n(r) = n0):
|
|
(33) |
mit Rg dem Radius eines geordneten Bereiches um jedes Streuzentrum. Es dominieren jeweils die cos-Terme und damit folgt als Verhältnis:
|
|
(34) |
Mit Rg
der
Schichtdicke = 30nm folgt für K
= 5 nm-1![]() ,
für K
= 100 nm-1
,
für K
= 100 nm-1
![]() .
Für amorphe und nanokristalline Stoffe ist die Vernachlässigung
von S3
also sicher gerechtfertigt.
.
Für amorphe und nanokristalline Stoffe ist die Vernachlässigung
von S3
also sicher gerechtfertigt.
Ende Einschub
Der Strukturfaktor ist definiert als S(K) = I(K) + 1.
Durch
eine Fouriertransformation von![]() (der
Strukturfunktion) erhält man die
reduzierte Paarkorrelation G(r) :
(der
Strukturfunktion) erhält man die
reduzierte Paarkorrelation G(r) :
|
|
(35) |
G(r)
entspricht einer mit r gewichteten Dichteschwankung um ein
Aufatom bei![]() .
Für Abstände
.
Für Abstände![]() ,
mit dem Nächstnachbarabstand r1, gilt für
die radiale Dichtefunktion
,
mit dem Nächstnachbarabstand r1, gilt für
die radiale Dichtefunktion![]() und
G(r) liefert in diesem Bereich n0. Über
eine Rücktransformation, bzw. Gl (23), von G(r) erhält
man wieder I(K).
und
G(r) liefert in diesem Bereich n0. Über
eine Rücktransformation, bzw. Gl (23), von G(r) erhält
man wieder I(K).
Abbruchoszillationen im Orstraum:
Bei der Berechnung von G(r) treten immer Abbruchoszillationen auf. Diese Oszillationen mit kleiner Wellenlänge treten zwangsläufig auf, da im Impulsraum nicht bis Unendlich integriert werden kann. Um diese Oszillationen zu reduzieren sollte man also den Integrationsbereich im Impulsraum so groß wie möglich wählen (Abbruchstelle bei großen K!). Der maximale Impulsübertrag Kmax gibt die Auflösung Δr=2π/Kmax im Ortsraum an [8]. Alle Strukturen unterhalb Δr sind Artefakte und auf Abbruchoszillationen durch Kmax zurückzuführen.
Möglichkeiten im Impulsraum:
die Abbruchstelle sollte entweder bei I(Kmax)=0 liegen, oder die Ableitung an dieser Stelle sollte Null sein
Kanten oder Sprünge in der Interferenzfunktion sollten vermieden werden (siehe guter Fit)
die „Parabel“ sollte einen glatten Übergang zur Interferenzfunktion haben
da Sprünge vermieden werden sollten, die Abbruchstelle aber meist einen verursacht wurde die Möglichkeit eingebaut ab der Abbruchstelle eine gedämpfte Sinuskurve anzulegen. Die Wellenlänge dieses Sinus ist gleich Kpe um zusätzliche Struktur im G(r) zu vermeiden. Allerdings ist das Ergebnis meist nicht befriedigend.
die untere Integrationsgrenze sollte bei K=0 nm-1 liegen.
Es gibt verschiedene mathematische und physikalische Ansätze um Abbruchoszillation zu vermeiden, bzw. zu identifizieren und „wegzurechnen“. Im folgenden werden einige genutzte Ansätze diskutiert.
Das eigentliche Problem ist die begrenzte Breite des Spektrums. Die Fouriertransformation erstreckt sich im korrekten Fall von -∞ bis +∞. Da nur ein begrenzter Bereich zur Verfügung steht integriert man folgendermaßen:
|
|
(36) |
Wobei R(K) eine Rechteckfunktion angibt, die dem zur Integration zur Verfügung stehendem Bereich entspricht :
|
|
(37) |
Daraus folgt:
|
|
(38) |
Sollte nun I(K) an der Stelle K=Kmax ungleich 0 sein, ist also an dieser Stelle eine Kante, werden zusätzliche Fourierkomponenten benötigt, welche diese Kante beschreiben. Diese zusätzlichen Fourierkomponenten sind die so genannten Abbruchoszillationen im Ortsraum. Diese Oszillationen hängen von Kmax und von der Intensität I(Kmax) an dieser Stelle ab. Der Beitrag im Ortsraum sollte sich einfach berechnen lassen:
|
|
(39) |
Beispiel: I(Kmax)=1, Kmax=100 nm-1
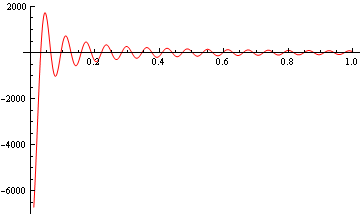
Abbildung
6: Abbruchoszillationen
Anmerkung:
in der Literatur wird für den Beitrag der Abbruchstelle angeben:
|
|
(40) |
(rote Kurve nach Gl. 39, blaue Kurve nach Gl. 40 mit C= 3000 multipliziert!)
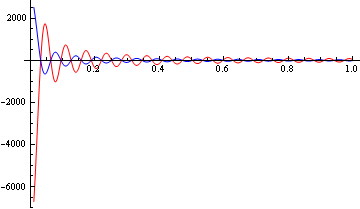
Abbildung
7: FT vom Kasten mit I(K)=
1 und Kmax=
100
Zur Reduzierung der Abbruchoszillationen ist es notwendig das einerseits gilt I(Kmax)=0 und es ist außerdem ein glatter Übergang notwendig, also möglichst dI(Kmax)/dK=0. Um dies zu erreichen gibt es verschiedene Ansätze. Alle diese Ansätze multiplizieren die originale Interferenzfunktion mit einer Korrekturfunktion, die dafür sorgen soll, das I(Kmax)=0 wird und für alle K>Kmax gilt I(K)=0.
|
|
(41) |
Alle diese Funktionen haben aber den Nachteil, das sie auch die Werte für K<Kmax ändern und damit Änderungen der Peakhöhen im G(r) bewirken und damit eine Änderung der Dichte nach sich ziehen. Zwei Korrekturfunktionen werden zur Zeit verwendet (sowohl bei uns, als auch von anderen Gruppen). Zum einen ist das die Lorchfunktion [8]
|
|
(42) |
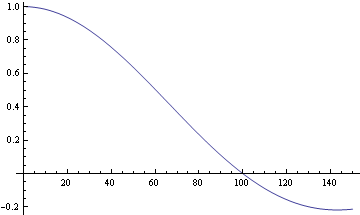
Abbildung
8: Lorch-Funktion
Allerdings ist bei dieser der Übergang bei Kmax nicht glatt.
Eine weitere genutzte Funktion ist eine Exponentialfunktion [3]:
|
|
(43) |
Mit einer wählbaren Konstanten α2, so daß gilt CE(K)≈0 .
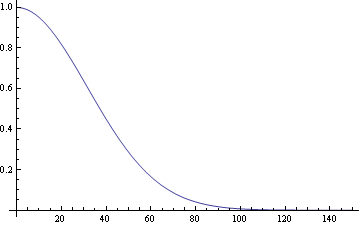
Abbildung
9: Exponentialfunktion
(α2=0,0005)
Hier ist
der Nachteil, dass es keine Konstante gibt, für die exakt gilt
CE(Kmax)=0,
so daß hier immer eine Kante auftritt.
Eine Möglichkeit den Nachteil des nicht glatten Überganges der Lorch-Funktion zu umgehen wäre diese zweimal anzuwenden
|
|
(44) |
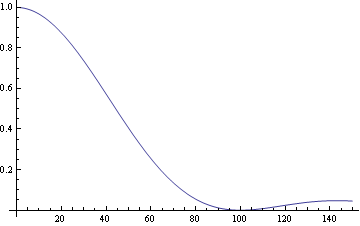
Abbildung
10: doppelte Lorch-Funktion
Eine weitere Fehlerquelle für Abbruchoszillationen ist natürlich die untere Integrationsgrenze. In EDDA ist diese aus programmtechnischen Gründen K=0 nm-1(dies verlangt die FFT). Sollte diese Grenze bei K>0 nm-1 liegen werden die „fehlenden“ Werte I(K)=0 gesetzt. Dies passiert übrigens auch bei einer Integration, die nicht per FFT durchgeführt wird, sondern als Summation von Kmin bis Kmax. Dabei kommt es natürlich ebenfalls zu einer Kante die Abbruchoszillationen im Ortsraum nach Gl. 39 (Kmax → Kmin) erzeugt. Da aber neben dem Wert I(Kmin) auch der Wert Kmin in die berechnung eingeht und dieser klein ist sind die resultierenden Abbruchoszillationen im allgemeinen klein und verschwinden bei Kmin=0 nm-1, obwohl hier natürlich ebenfalls eine kante mit der Höhe I(K=0) besteht. Untersuchungen zur unteren Integrationsgrenze wurden auch bereits von [9] durchgeführt.
Abbruchoszillationen im Impulsraum:
Bisher wurde nur über Abbruchoszillationen im Ortsraum diskutiert. Es sollten aber natürlich auch Abbruchoszillationen bei der Rücktransformation vom Ortsraum in den Impulsraum auftreten, da auch hier nur ein endlicher Bereich für die Transformation zur Verfügung steht.
Interessanterweise sind diese Oszillationen beim Transformieren nicht sichtbar. Warum nicht?
Analog zu den Abbruchoszillationen im Ortsraum kann man auch diejenigen im Impulsraum berechnen:
|
|
(45) |
Mit R(r) einer Rechteckfunktion im Ortsraum und der Amplitude R0. Damit ergibt sich:
|
|
(46) |
Allerdings sind diese Oszillationen sehr klein, da einerseits R0 sehr klein ist (R0<1) und durch den Faktor K-2 die Oszillationen nur für kleine K nennenswerte Werte haben.
Beispiel: Al45Cr55: R0 = -0,86, rm = 3,83nm
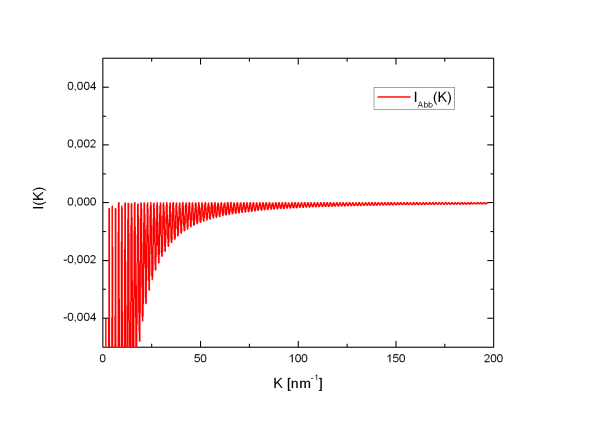
Abbildung
11:
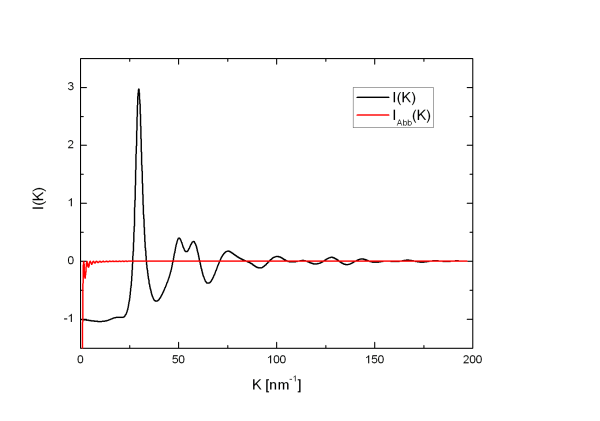
Abbildung
12:
Die Abbruchoszillationen sind sogar schon unterhalb eines möglichen Vormaximums zu vernachlässigen, so dass davon auszugehen ist, das Abbruchoszillationen im Impulsraum keinen Fehler verursachen, weder in zusätzlichen Maxima, noch in der Verschiebung von Maxima und auch nicht in einer Änderung der Intensität.
Aus G(r) erhält man die Paarkorrelation g(r):
|
|
(47) |
Für die Paarkorrelation gilt die Normierung:
|
|
(48) |
Aus der Ornstein-Zernike Gleichung:
|
|
(49) |
folgt die direkte Korrelationsfunktion c(r) über die totale Korrelationsfunktion h(r) [10].
Die Fourier-transformierte von h(r) ist:
|
|
(50) |
Daraus folgt sofort:
|
|
(51) |
Mit der totalen Korrelationsfunktion kann man die Kompressibilität berechnen, die im Strukturfaktor im Wert für S(K=0) enthalten ist.
|
|
(52) |
Für die Strukturanalyse wichtig ist weiterhin die radiale Verteilungsfunktion (RDF) D(r):
|
mit |
(53) |
Sie
gibt an, wie viele Atome in einer Kugelschale![]() um
ein beliebiges Aufatom liegen. Der Faktor
um
ein beliebiges Aufatom liegen. Der Faktor![]() in
Gl. (53). entspricht der Oberfläche dieser Kugelschale. Im
Zweidimensionalen wäre der Faktor
in
Gl. (53). entspricht der Oberfläche dieser Kugelschale. Im
Zweidimensionalen wäre der Faktor![]() entsprechend
dem Umfang eines Kreises und im Eindimensionalen dem Abstand
entsprechend
dem Umfang eines Kreises und im Eindimensionalen dem Abstand![]() .
Die Fläche unter dem ersten
Maximum der RDF ergibt die
Zahl der nächsten Nachbaratome (Koordinationszahl, Nc)
[6].
.
Die Fläche unter dem ersten
Maximum der RDF ergibt die
Zahl der nächsten Nachbaratome (Koordinationszahl, Nc)
[6].
|
|
(54) |
Wobei r1 den Abstand bis zum ersten nächsten Nachbarn angibt. Allgemein kann man schreiben:
|
|
(55) |
Diese Funktion oszilliert um
|
|
(56) |
Die Differenz zwischen (55) und (56), reduzierte Teilchenzahl-Funktion [11] berechnet sich zu:
|
|
(57) |
mit der reduzierten radialen Dichtefunktion [11]:
|
|
(58) |
Die
reduzierte Teilchenzahlfunktion f(r) oszilliert um -1, Für
r-Werte unterhalb des ersten nächsten Nachbarn r1
gilt analog (35)![]() und
es gilt
und
es gilt
|
|
(59) |
Daraus lässt sich die experimentelle Teilchenzahldichte n0 bestimmen zu [11]:
|
|
(60) |
Allerdings ergeben sich nur für Schmelzen korrekte Werte, für amorphe Legierungen liegen die berechneten Werte zu niedrig. Aus (55) und (60) ergibt sich ebenfalls eine Möglichkeit der Bestimmung der Koordinationszahlen aus der experimentellen Teilchenzahldichte:
|
|
(61) |
bzw. für verschiedene Koordinationssphären:
|
|
(62) |
Aus
der RDF ergibt sich die radiale Dichteverteilung![]() zu:
zu:
|
|
(63) |
1.2. Übersicht der Formeln
Ortsraum:
|
Name |
Formelzeichen |
math. Beziehungen |
Einheit |
|---|---|---|---|
|
reduzierte Paarkorrelation |
G(r) |
(Oszillation um 0) |
|
|
Paarkorrelation |
g(r) |
(Oszillation um 1) |
|
|
radiale Dichteverteilung |
n(r) |
(Oszillation um |
|
|
radiale Verteilungsfunktion (RDF) |
D(r) |
(Oszillation um |
|
|
Koordinationszahl |
|
|
|
|
Reduzierte radiale Dichtefunktion |
H(r) |
|
|
|
reduzierte Teilchenzahlfunktion |
f(r) |
|
|
Impulsraum:
|
Name |
Formelzeichen |
math. Beziehungen |
Einheit |
|---|---|---|---|
|
Streuintensität |
|
|
|
|
Untergrund |
U(K) |
|
|
|
Streuspektrum |
|
|
|
|
Formfaktor |
f(K) |
|
|
|
Interferenzfunktion |
I(K) |
(Oszillation um 0) |
|
|
Strukturfaktor |
S(K) |
(Oszillation um 1) |
|
|
Strukturfunktion |
|
|
|
Literaturverzeichnis
[1] P.A. Doyle, P.S. Turner; Acta. Cryst., (1967) 390
[2] Jiang Jian-Sheng, Li Fang-Hua; Act. Phys. Sinica, 6 (1984) 849
[3] B. E. Warren; X-Ray Diffraction, Addison-Wesley, Reading, MA (1968)
[4] H. Leitz; Dissertation (1979)
[5] J. Krogh-Moe; Acta Cryst., (1956) 951
[6] Y. Waseda; The Structure of Non-Crystalline Materials, McGraw-Hill, New York (1980)
[7] C.N.J. Wagner; Diffraction Analysis of Liquid Metals and Alloys, (1972)
[8] E. A. Lorch; J. Phys. C, 2 (1969) 229
[9] W. Hoyer, I. Kaban, Th. Halm; J. Optoelectronics and Advanced Materials, 3 (2001) 255
[10] E. Guarini, G. Casanova, U. Bafile, F. Barocchi; Phys. Rev. E, 6 (1999) 6682
[11] A. Il`inskii, I. Kaban, W. Hoyer, A. Shpak, L. Taranenko; J. Non. Cryst, (2004) 39-44