Physik

Herleitung ohne Integralrechnung
Kraft
kinetische Energie
Rotationsenergie, Trägheitsmoment
Zentripedalkraft

Bernoulligleichung

Ladung im elektrischen Feld

Die Einheit „Elektronenvolt“


Mechanik

Formelzeichen
a- Beschleunigung
v- Geschwindigkeit
t- Zeit
s- Weg
E- Energie
F- Kraft
p- Impuls
m- Masse


Grundformeln

1.

2.

3.

4.

Geschwindigkeit-Zeit-Gesetz
Die ganze Mechanik baut sich auf einigen wenigen Grundformeln auf. Die erste, die wir benutzen wollen ist:

umgestellt nach dv ergibt sich:



das kann man jetzt integrieren und erhält:


genau die Formel, die in Formelsammlungen für die Geschwindigkeit einer beschleunigten Bewegung angegeben wird.
Hinweis: v₀ da es eine unbestimmte Integration ist und deshalb eine Integrationskonstante von nöten ist. Diese muß als Einheit natürlich die Einheit einer Geschwindigkeit haben, also eben die Anfangsgeschwindigkeit.
Und wenn die Bewegung nicht beschleunigt ist? Dann ist a = 0 und damit v = v₀, der Anfangsgeschwindigkeit.


Weg-Zeit-Gesetz

Jetzt wissen wir wie groß die Geschwindigkeit ist und wollen wissen welchen Weg man damit zurücklegen kann.  Die Geschwindigkeit ist außerdem (Grundformel 2):


das integrieren wir wieder und erhalten:


den Weg, den ein Körper mit einer bestimmten Beschleunigung, einer bestimmten Anfangsgeschwindigkeit in einer bestimmten Zeit zurücklegt.
Hinweis: s₀ wieder wegen unbestimmter Integration.

Einschub:

Alternative Herleitung ohne Integral

Für alle diejenigen, die mit Integralrechnung auf Kriegsfuß stehen, oder in der Schule keine Integralrechnung hatten, folgt hier eine Herleitung auf geometrischer Basis (was letzten Endes die Grundlage für Integralrechnung ist)
Betrachten wir uns erst mal ein Geschwindigkeits-Zeit-Diagramm einer beschleunigten Bewegung, mit einer Anfangsgeschwindigkeit:

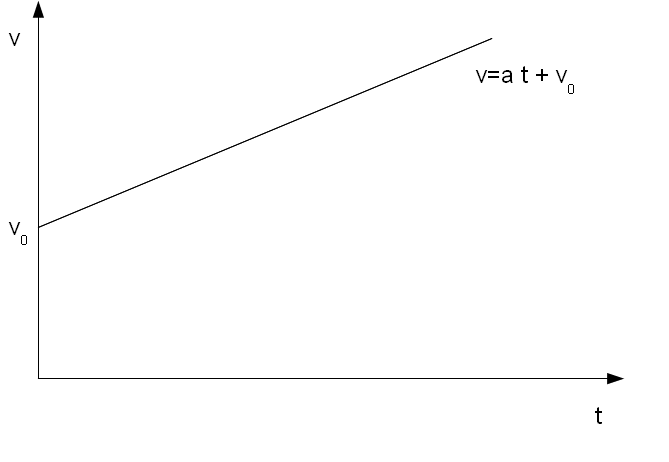
Wie wir wissen ist der Weg die Fläche unter dem Graphen. Teilen wir diese Fläche nun in geometrisch gut zu beschreibende Teile auf, also in ein Dreieck und ein Viereck:

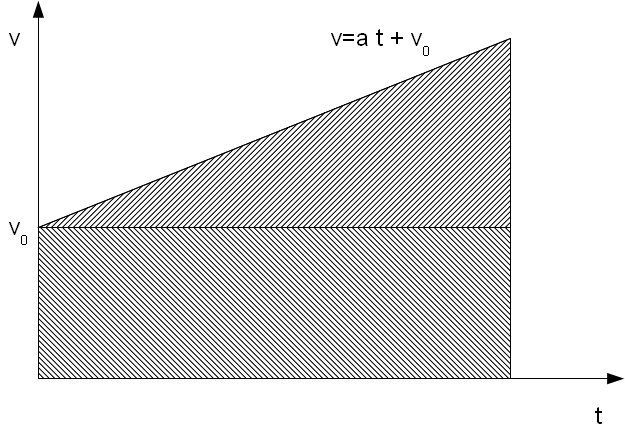
Das Rechteck hat eine Fläche (Fläche A ist gleich Weg s) von und das Dreieck eine Fläche von. Das Stückist aber gerade(siehe Abbildung), also ist die Dreiecksfläche. Die Summe aus beiden Wegen ist der Gesamtweg:

Genau das Ergebnis, was wir erwartet haben. Einziger Unterschied zur Herleitung mittels Integralen ist, das man hier den Anfangsweg „per Hand“ dazu addieren muß.

Ende Einschub

Wenn die Beschleunigung a = 0 ist, also eine gleichförmige Bewegung vorliegt, ist der erste Summand Null und damit s = v₀ t + s₀.
Da fragt man sich doch warum in Formelsammlungen für die verschiedenen Bewegungsarten jeweils einzelne Formeln angegeben werden, obwohl zwei reichen?

Was ist aber, wenn man keine Translation vorliegen hat sondern eine Rotation?
Antwort: Man ersetzt einfach die Beschleunigung durch die Winkelbeschleunigung, Geschwindigkeit durch Winkelgeschwindigkeit und Weg durch Winkel, fertig.

Wurf (senkrecht, waagerecht und schräg)

Wenden wir uns erstmal einem senkrechten Wurf nach oben oder unten (auch freier Fall genannt) zu. Da hier nur eine Bewegungsrichtung, eben nach oben oder unten, die z-Richtung, eine Rolle spielt braucht man hier noch keine Vektoren. Diese Bewegung ist eine Bewegung im Erdschwerefeld und damit eine beschleunigte Bewegung. Die Beschleunigung a ist hier natürlich die Erdbeschleunigung g = 9,81... m/s². Da diese Beschleunigung nach unten wirkt ist a = -g.
Das ist streng genommen nicht ganz korrekt, da sich die Erdbeschleunigung mit der Höhe ändert (wird kleiner), aber näherungsweise und für "kleine" Höhen kann man das so verwenden.
Und schon kann man die Formel für einen senkrechten Wurf mit dem allgemeinen Weg-Zeit-Gesetz aufstellen.

Hinweis: In Tafelwerken wird als "Weg" die Höhe bezeichnet, was sinnvoll ist, da sich ja die Höhe ändert, aber es ist im weitesten Sinn trotzdem ein Weg.

Möchte man wissen, wie die Geschwindigkeit in einer bestimmten Höhe ist nimmt man das allgemeine Geschwindigkeits-Zeit-Gesetz von oben her und ersetzt nur a durch -g und fertig.


Bei einem waagerechten Wurf ist die Situation etwas anders. Hier hat man eine Bewegung in zwei Richtungen, einmal in x-Richtung (parallel zur Erdoberfläche) und in z-Richtung, eben weil wieder die Erdanziehung auf den Körper wirkt.
In x-Richtung gibt es bekanntlich keine Beschleunigung, also ist im allgemeinen Weg-Zeit-Gesetz a=0 und es ergibt sich:


In z-Richtung wirkt die Erdbeschleunigung und damit wird a=-g, v₀ = 0 (ACHTUNG: hier ist v₀ in z-Richtung gemeint, da es ein waagerechter Wurf ist, ist diese Komponente natürlich Null!). Damit ergibt sich:


Verblüffend, oder? Was man mit dem allgemeinen Weg-Zeit-Gesetz und Geschwindigkeit-Zeit-Gesetz alles machen kann.


Kraft
Die Kraft ist allgemein die Impulsänderung mit der Zeit (Grundformel 3). Da der Impuls Geschwindigkeit mal Masse ist folgt sofort (unter Benutzung von Grundformel 1):


Der erste Summand gibt die Kraft an, die auf einen Körper wirkt, wenn sich dessen Masse ändert (bspw. bei einer Rakete, die ihren Treibstoff verbrennt und nach hinten rausbläst). Da dieser Fall äußerst selten ist, wird dieser Summand im Alltag meistens Null und übrig bleibt der zweite Summand, welcher die bekannte Beziehung F=ma angibt.

Anmerkung: da die Kraft die Impulsänderung pro Zeit angibt wird die Kraft auch Impulsstrom genannt.

kinetische Energie

Damit können wir nun für einen bewegten Körper angeben wo und wie schnell er ist. Nun wollen wir wissen welche Bewegungsenergie er hat.
Dazu benötigen wir Grundformel 4:


Die Energie ist das Integral der Kraft über den zurückgelegten Weg. Die Kraft kennen wir aus dem 3. Newtonschen Axiom (siehe oben mehr):

die Beschleunigung und Geschwindigkei ersetzen wir über


und erhalten


das ergibt

die kinetische Energie.

Potentielle Energie

Die potentielle Energie läßt sich am einfachsten herleiten. Dazu brauchen wir wieder die Grundformel 4:

und mit bzw., da wir uns ja im Erdschwerefeld bewegen und außerdem ersetzen wir den Weg s noch durch die Höhe h ergibt sich.

die potentielle Energie.

Anmerkung: im realen Fall ist die Erdbeschleunigung von der Höhe abhängig. Sie nimmt nämlich mit der Höhe ab und zwar gemäß dem Newtonsche Gravitationsgesetz zwischen zwei Körpern.

(γ - Newtonsche Gravitationskonstante, m, M – Massen der beiden Körper, r – Abstand der Massenmittelpunkte)

Ein Vergleich mit ergibt:

(mit r dem Radius des Körpers, ergibt im Falle der Erde an der Oberfläche den bekannten Wert von g =9.81 m/s²)

Bzw. mit der Höhe h:

(R_E – Erdradius)

ergibt das:

(sogar richtigerweiße Minus, da Energie frei werden muß, wenn die Höhe abnimmt)

Rotationsenergie, Trägheitsmoment

Nehmen wir an eine Punktmasse rotiert um einen Punkt mit der Geschwindigkeit v. Diese Punktmasse hat natürlich eine kinetische Energie.


Ersetzen wir die Geschwindigkeit v durch die Winkelgeschwindigkeit


Jetzt lassen wir nicht eine Punktmasse rotieren, sondern viele. Die Gesamtenergie ist also die Summe der einzelnen kinetischen Energien. Damit ergibt sich:


Bei einem Körper geht man zum Integral über:


Jetzt definiert man das Trägheitsmoment J:


und erhält:


die Rotationsenergie.


Zentripedalkraft

Nehmen wir Grundformel 4 zur Hand und formen diese etwas um erhalten wir:


Setzten wir in diese Formel die Rotationsenergie ein: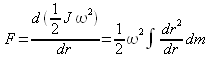


Daraus folgt durch Ausführung der Integration über dm:


die Zentripedalkraft.

Bernoulligleichung

Wie wir wissen ist der Druck per Definition Kraft pro Fläche, also:

da folgt durch simples einsetzen:

. Da A eine Fläche ist, die mit einer weiteren Länge (s) multipliziert wird ergibt das zusammen ein Volumen, also:

. Jetzt erinnern wir uns an die Energieerhaltung, die Gesamtenergie ist immer konstant. Die Gesamtenergie setzt sich unter anderem aus kinetischer und potentieller Energie zusammen und einem „Energierest“:

. Diese Gleichung teilen wir jetzt durch das Volumen V:

. Zuletzt ersetzen wir noch m und V durch die Dichte () und erhalten:

, die Bernoulligleichung, die also im Grunde nichts weiter ist als die Energieerhaltung.

Ladung im elektrischen Feld

Die elektrische Feldstärke in einem homogenen elektrischen Feld, z.B. in einem Plattenkondensator, hängt nur von der Spannung und dem Abstand ab.

Die Kraft, die in solch einem Feld auf eine Ladung wirkt ist. Da die Kraft aber auch allgemeinfolgt durch einsetzen

Nun ersetzen wir noch die Beschleunigung (s. Oben) und kürzen den Weg/Abstand

Der Ausdruck links vom Gleichheitszeichen sollte uns bekannt werden, das ist nämlich nichts anderes, als die kinetische Energie und damit folgt kurz:

, und fertig!

Nehmen wir mal an wir haben ein Elektron in einem Feld mit der Spannung U=1V. Die Ladung ist dann die Elementarladung des Elektrons, also q = e = −1,602176487 10^-19 C. Setzen wir das in obige Gleichung ein steht da:

Als Einheit muß natürlich Joule rauskommen, die Einheit der Energie:

klappt also und damit steht in obiger Formel nichts anderes, als:

,

oder in Worten: Ein Elektronenvolt ist gleich (-)1,602176487 10^-19 J.

wird fortgesetzt.......................